多头自注意力机制与Transformer

2024.12.06整理

自注意力机制（计算过程见：https://zhuanlan.zhihu.com/p/338817680 3.2节与3.3节）

有$M$个特征（或者单词）（又叫seq_len: 句子长度,即单词数量）

每个单词用一个$d$维向量表示，记作矩阵 $X_{M*d}$ ，矩阵有$M$行，每行对应一个特征/单词，每行是$d$维。

Self-Attention 的输入是矩阵$X$，则可以使用线性变换矩阵$W_Q,W_K,W_V$计算得到$Q,K,V$矩阵。

$W_Q,W_K,W_V$的维度是 $d*d^{\prime}$ ，得到的$Q,K,V$矩阵的维度是 $M*d'$ 。 $X, Q, K, V$的每一行都对应一个单词。

矩阵乘法：

$Q=X×W_Q$

$K=X×W_K$

$V=X×W_V$

然后计算$Score(Q,K^T)$，即矩阵相乘$QK^T$，维度是$M*M$，元素$a_{ij}$代表第$i$个单词和第$j$个单词之间的关联程度（attention强度/权重/attention系数/相似性）。

（为了防止$a_{ij}$过大，所有的$a_{ij}$都要除以$\sqrt{d’}$）

再对$QK^T$的每一行做$softmax$，使得每行各元素之和都为1.

得到新的维度为$M*M$的矩阵$softmax(QK^T)$。

再和矩阵$V$进行元素相乘，得到最终的输出矩阵$Z$，$Z=softmax(QK^T) × V$

$Z$的维度是$M*d’$

矩阵$X,V,Z$的每一行都是对每个单词的向量表示，都有$M$行，因此该过程简单来讲就是$X→V→Z$，

得到最终的矩阵$Z$，$Z$的每行是作为对每个单词的新向量表示。

每个单词的新向量，都是融合了其它单词信息的新向量。而$X$的每行是没有融合其他单词信息的旧向量。

计算公式写成：

自注意力机制的输出为矩阵$Z$：

$Z=Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d'}})V$

多头自注意力机制

（一组头：就是一组$Q \ K \ V$矩阵，多头有多组$Q \ K \ V$矩阵，从而得到不同的输出矩阵$Z_i$）

【不同的头又叫不同的“子空间”，头=子空间，可理解为不同的角度】

【如果想从多个角度看，可以用多个头，即换不同的矩阵$W_Q,W_K,W_V$得到不同的$Q,K,V$，然后得到不同的输出矩阵$Z_i$】

多头自注意力机制Multi-Head Attention，是由多个自注意力机制Self-Attention组成的。

Multi-Head Attention 包含多个 Self-Attention 层，

首先将输入X分别传递到 h 个不同的 Self-Attention 中，计算得到 h 个输出矩阵$Z_i$。

比如当 h=8 时，此时会得到 8 个输出矩阵$Z_i$。

得到 8 个输出矩阵$Z_1$~$Z_8$之后，Multi-Head Attention 将它们拼接在一起 (Concat)，然后传入一个Linear层，得到 Multi-Head Attention 最终的输出Z。

（每个$Z_i$的维度是 $M*d'$ ，与$X$的维度不同；而多头自注意力机制的最终输出$Z$的维度是 $M*d$ ，与$X$的维度相同。）

三种注意力机制（Encoder一种，Decoder两种）

Encoder块的数量，Decoder块的数量：N_e N_d 是超参数，可设置

Transformer模型详解（图解最完整版）

Encoder一种：每个Encoder块里面有，缩放点积自注意力

第一个Encoder块的输入：源序列 $X_{M*d}$ ，算出当前Encoder块的Q K V，输出是 $Z_{M*d}$

第2~n个Encoder块的输入：上一个Encoder块的输出 $Z_{M*d}$ ，算出当前Encoder块的Q K V，再输出新的 $Z_{M*d}$

第n个Encoder块的输出：编码信息矩阵C，维度也是 $C_{M*d}$

Decoder两种：每个Decoder块里面有，掩码自注意力机制，交叉注意力机制

第一个Decoder块的输入：目标序列 $X^{goal}_{M*d}$ 【不是源序列 $X_{M*d}$ 】和C，输出是 $Z_{M*d}$

第2~n个Decoder块的输入：上一个Decoder块的输出 $Z_{M*d}$ 和C，再输出新的 $Z_{M*d}$

第n个Decoder块的输出： $Z^{final}_{M*d}$

后续过程：

将 $Z^{final}_{M*d}$ 通过一个线性层（Linear），维度从 [M, d] 变为 [M, vocab_size]。（M个单词，每个单词有vocab_size种可能）

现在，我们得到了一个矩阵，可以称为 Logits。它的每一行（共M行）对应目标序列中的一个位置，每一行的向量（长度为 vocab_size）代表了在该位置词汇表中所有单词的得分（logits）

对 Logits 矩阵的每一行独立地进行 Softmax 操作，得到 Probs矩阵，维度是[M, vocab_size]，但现在每一行都变成了一个概率分布（该行所有元素之和为1）。

对于 Probs 矩阵的每一行（即目标序列的每一个位置），选择概率值最大的那个元素所在的列索引。

得到一个包含 M 个索引值的向量，形状为 [M]。每个索引值对应词汇表中的一个单词。

将这 M 个索引值通过一个查找表，映射回词汇表中对应的实际单词。

最终输出： 得到一个由 M 个单词组成的序列，这就是模型生成的整个目标句子（例如翻译结果）。

上面是非自回归的过程！！Decoder在训练时是非自回归，推理时是自回归。

推理时：

	Encoder（编码器侧）	Decoder（解码器侧）
运行次数	只运行1次	运行M次（循环生成目标序列的每一个词）
输入	完整的源序列 `[M_src, d]`	不断增长的目标序列：`[1, d]` -> `[2, d]` -> … -> `[M, d]`
输出	编码信息 `C [M_src, d]`	下一个词的概率分布 `[vocab_size]`
工作状态	提前完成，结果被缓存	循环工作，串行生成

输入Encoder的源序列：可以理解为输入进LLM的prompt。

输入Decoder的目标序列：

训练时【非自回归】： 第一个Decoder块的输入是完整的目标序列 X_goal [M, d]（并使用掩码确保并行计算时不泄露未来信息）。
推理时【自回归】： 第一个Decoder块的输入是起始符 [<sos>]，形状为 [1, d]。每次生成一个新词，就将其拼接到当前输入序列的末尾，输入长度从 [1, d] -> [2, d] -> … -> [M, d]，逐步增加，直到生成结束符。

训练时（非自回归）	推理时（自回归）
一次处理整个序列 `[T, d_model]`	逐步生成，每次只处理到当前序列 `[当前长度, d_model]`
线性层输出 `[T, vocab_size]`	每次只取最后一个向量，维度是 `[vocab_size]`
得到T个概率分布，一次性选出T个词	得到1个概率分布，只选1个词，然后循环

所以，Decoder在每一步只生成一个词。它利用整个已生成的序列作为上下文，但只输出下一个词的概率分布。

特性	训练 (Training)	推理 (Inference)
模式	非自回归 (Parallel)	自回归 (Sequential)
输入	完整的目标序列（右移一位）	模型自己之前生成的结果
输出	整个序列的概率分布 `[T, vocab_size]`	下一个词的概率分布 `[vocab_size]`维向量
速度	快（并行计算）	慢（串行计算）
关键	使用掩码和教师强制	使用自回归循环生成

掩码自注意力机制的输入输出和缩放点积自注意力是一样的，唯一区别就是在计算得到的Q*K^T上面，加了掩码，（计算softmax之前）。

交叉自注意力机制：

当前Decoder块的Q用上一个Decoder块的输出 $Z_{M*d}$ 计算得到。

当前Decoder块的K V用C计算得到。

什么是多头，以及其他网络结构细节

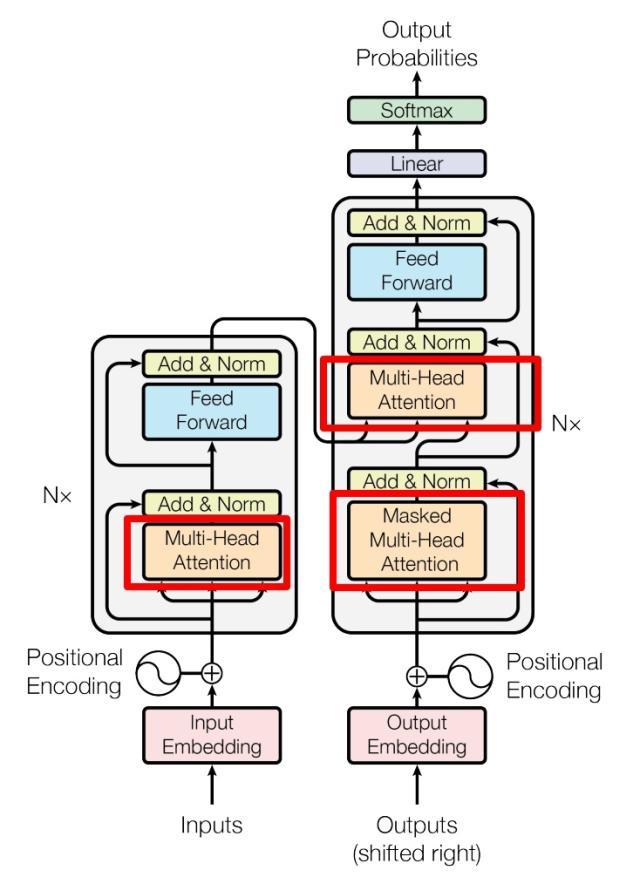
多头注意力的意思：

一个head=一个（Q,K,V）

多头=多个并行的（Q,K,V）

单头的情况：

有 $M$ 个特征（或者单词）（又叫seq_len: 句子长度,即单词数量）

每个单词用一个$d$维向量表示，记作矩阵 $X_{M*d}$ ，矩阵有$M$行，每行对应一个特征/单词，每行是$d$维。

Self-Attention 的输入是矩阵$X$，则可以使用线性变换矩阵$W_Q,W_K,W_V$计算得到$Q,K,V$矩阵。

$W_Q,W_K,W_V$的维度是 $d*d$ ，得到的$Q,K,V$矩阵的维度是 $M*d$ 。 $X, Q, K, V$的每一行都对应一个单词。

矩阵乘法：

$Q=X×W_Q$

$K=X×W_K$

$V=X×W_V$

（为了防止$a_{ij}$过大，所有的$a_{ij}$都要除以$\sqrt{d}$）

再对$QK^T$的每一行做$softmax$，使得每行各元素之和都为1.

得到新的维度为$M*M$的矩阵$softmax(QK^T)$。

再和矩阵$V$进行元素相乘，得到最终的输出矩阵$Z$，$Z=softmax(QK^T) × V$

$Z$的维度是$M*d$

多头的情况：【变化：单个注意力机制 → 多头注意力机制】

将原始的 d 维特征空间分割成 h 个头，这 h 个头可以完全并行地计算自注意力。

注意：不是直接对输入矩阵 X 进行划分！！并不是划分输入 X（比如把 (M, d) 的矩阵切成 h 个 (M, d/h) 的矩阵）。

而是把完整的X ∈R^[M,d] 都输入到并行的h个头中。

比如有h个头，是并行的，即h组（Q,K,V）：

对于每一个头 i (i from 1 to h)，我们都有其对应的查询（Q）、键（K）、值（V）的线性变换投影矩阵：

$W_Q^i ∈ ℝ^(d × d_Q)$
$W_K^i ∈ ℝ^(d × d_K)$
$W_V^i ∈ ℝ^(d × d_V)$

对于每个头，我们独立地进行线性投影：

$Q^i = X · W_Q^i → 维度: (M, d_Q)$
$K^i = X · W_K^i → 维度: (M, d_K)$
$V^i = X · W_V^i → 维度: (M, d_V)$

注意：有 $d_Q=d_K=d_V=d/h$

比如d=512，有h=8个头，则每个头内部的 $d_Q=d_K=d_V=512/8=64$

之后一步步计算，每个头的输出$Z^i$的维度是 $M*d_V$

h个头，得到h个维度为 $M*d_V$ 的 $Z^i$ ，接下来：

①将这 h 个头的输出拼接起来。（ $d_V*h=d$ ）

h个 $Z^i$ 拼接，得到最终的Z，维度为 $M*d$

②线性投影：

将拼接后的结果 Z 通过一个可学习的线性变换 W^O

操作： Output = Z · W^O
参数矩阵 W^O 的维度： (h * d_v, d) 也就是 (d, d)（因为 h * d_v = d）。
输出维度： (M, d) · (d, d) = (M, d)

这一步的目的是让模型自由地学习和融合来自所有头的信息。

最终，该多头注意力的输出是 $MultiHeadOutput_{M*d}$ ，维度和输入 $X_{M*d}$ 是一样的。

（ $MultiHeadOutput_{M*d}$ 就是我上文【三种注意力机制（Encoder一种，Decoder两种）】中的 $Z_{M*d}$ ）

注意力后的Feed Forward层：

FFN对注意力层的输出 Z（维度 (M, d)）进行两步操作。

输出是 $FFN(Z) = max(0, Z W_1 + b_1) W_2 + b_2$ 。

FFN(Z) 的维度仍然是 (M, d)

W_1 是一个 (d, d_ff) 的矩阵，b_1 是维度 d_ff 的向量。
W_2 是一个 (d_ff, d) 的矩阵，b_2 是维度 d 的向量。

d_ff > d，即先升维再降维。

ReLU激活函数 (max(0, x)) 提供了至关重要的非线性变换能力。

FFN就是一个“升维 → 非线性激活 → 降维”的处理过程。

注意力后面的Add & Norm 和Feed Forward后面的Add & Norm：

Add & Norm 层由 Add 和 Norm 两部分组成，其计算公式如下：

其中 X表示 Multi-Head Attention 或者 Feed Forward 的输入，MultiHeadAttention(X) 和 FeedForward(X) 表示注意力机制，和FFN的输出 (输出与输入 X 维度是一样的，都是M*d，所以可以相加)。

Add指 X+MultiHeadAttention(X)，是一种残差连接，通常用于解决多层网络训练的问题，可以让网络只关注当前差异的部分，在 ResNet 中经常用到。

Norm指 Layer Normalization，通常用于 RNN 结构。

Transformer其他细节：

见下面，写的易懂，要多看！

https://zhuanlan.zhihu.com/p/338817680

补充笔记：

Transformer 本身是不能利用单词的顺序信息的，因此需要在输入中添加位置 Embedding！

$PE_{pos,2i}，PE_{pos,2i+1}$，这里的$2i,2i+1$是维度索引，即分量，是在计算奇数编号和偶数编号的分量的值。

层归一化（Layer Normalization）和批归一化（Batch Normalization，BN）的区别：

假设输入矩阵为$X_{n*d}$，

n 是批量大小（batch size），代表有n个单词/物品，一行对应一个；

d 是每个单词/物品的特征数量。

Layer Normalization 的步骤如下：

计算均值： 对每个样本（行）计算特征的均值。对于第$i$个样本$\mathbf{x}_i = (x_{i1}, x_{i2}, …, x_{id})$，均值是：
$\mu_i = \frac{1}{d} \sum_{j=1}^{d} x_{ij}$
计算方差：对每个样本计算特征的方差：
$\sigma_i^2 = \frac{1}{d} \sum_{j=1}^{d} (x_{ij} - \mu_i)^2$
归一化：使用均值和方差对每个特征进行归一化：
$\hat{x}_{ij} = \frac{x_{ij} - \mu_i}{\sqrt{\sigma_i^2 + \epsilon}}$
其中 $\epsilon$ 是一个非常小的常数，用于防止除零错误。
缩放和平移：在归一化后，Layer Normalization 会引入两个可学习的参数 $\gamma$ 和 $\beta$，分别用于缩放和平移。最终输出是：
$y_{ij} = \gamma_j \hat{x}_{ij} + \beta_j$
其中 $\gamma_j$ 和 $\beta_j$是为每个特征（每个列）学习到的参数。

总结：

Layer Normalization 对每个样本的特征进行归一化。

它不像 Batch Normalization 依赖于批量数$n$，而是对每个样本单独归一化，适用于处理序列数据（如RNN、Transformer等），尤其在批量大小较小或单个样本处理时。

批归一化的步骤：

计算批次均值：对整个批次的每个特征维度（列）计算均值，即计算每一列（特征）在批次中所有样本的均值。对于第$j$个特征维度，它的批次均值是：
$\mu_j = \frac{1}{n} \sum_{i=1}^{n} x_{ij}$
其中，$x_{ij}$是第 $i$个样本在第$j$个特征维度上的值。
计算批次方差：对整个批次的每个特征维度（列）计算方差，即计算每一列（特征）在批次中所有样本的方差。对于第$j$个特征维度，它的批次方差是：
$\sigma_j^2 = \frac{1}{n} \sum_{i=1}^{n} (x_{ij} - \mu_j)^2$
这里的$\sigma_j^2$是第$j$个特征维度在批次中的方差。
归一化：使用计算得到的均值$\mu_j$和方差 $\sigma_j^2$对每个样本的每个特征进行归一化处理。对于第$i$个样本在第$j$个特征维度上的归一化值：
$\hat{x}_{ij} = \frac{x_{ij} - \mu_j}{\sqrt{\sigma_j^2 + \epsilon}}$
这里$\epsilon$ 是一个很小的常数，用来防止方差为零时出现除零错误。
缩放和平移（可选）：批归一化通常会引入两个可学习的参数：$\gamma_j$和$\beta_j$，分别用于缩放和偏移归一化后的值。这样做的目的是让网络有更大的表达能力，因为在训练过程中，经过归一化的输出可以通过这些参数重新调整回原始尺度。
$y_{ij} = \gamma_j \hat{x}_{ij} + \beta_j$
其中，$\gamma_j$是缩放因子，$\beta_j$是偏移因子，通常会初始化为1和0。

批归一化通常在卷积神经网络（CNN）和全连接层网络（FCN）中使用。

层归一化：是在每个样本的特征维度上进行归一化，每个样本独立归一化。每行进行归一化、

批归一化：是在整个批次上对每个特征维度进行归一化，考虑了批次中的所有样本。每列进行归一化。

每个Decoder Block：

包含两个 Multi-Head Attention 层。
第一个 Multi-Head Attention 层采用了 Masked 操作：
- 在计算得到$QK^T$，对$QK^T$的每一行做$softmax$之前，
- 先使用Mask矩阵，将$QK^T$变成Mask $QK^T$，
- 再对Mask $QK^T$的每一行做$softmax$。
第二个 Multi-Head Attention 层的K, V矩阵使用 Encoder 的编码信息矩阵C进行计算得出，而Q使用上一个 Decoder block 的输出计算得出。

Encoder和Decoder的输入输出：

Encoder的输入：源文本的单词表示矩阵$X_{n,d}$，如“我有一只猫”，共4个单词

Encoder的输出：信息编码矩阵$C_{n,d}$，与$X$的维度一致， $（n=seq\_len,d=emd\_size）$

Decoder的输入：目标文本的单词表示矩阵$X_{n,d}$，如”<Begin> I have a cat”，共5个单词

（Encoder的输出矩阵$C$会输入到Decoder的第二个$Multi-Head \ Attention$中）

Decoder的输出：预测的单词序列，如“I have a cat <end>”。

Transformer和多头注意力机制